Exponential Functions and Logarithmics Functions
are INVERSES of eachother.
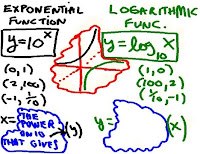 y = log base 10 of x
y = log base 10 of xI hope to help students and future Math Teachers with a variety of Mathematics Topics by sharing methods and ideas that I used during my 40 year career. Feel free to request a Math topic (or a specific problem's solution) to be added to the blog!
 y = log base 10 of x
y = log base 10 of x
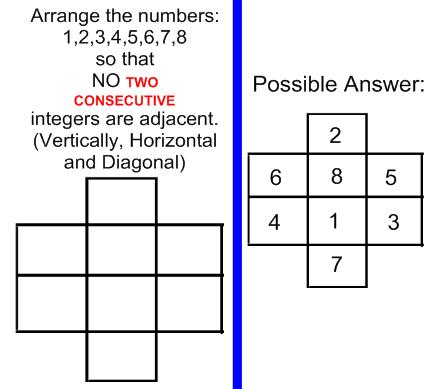



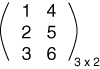
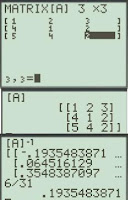
 "X" is wrapped first with
"X" is wrapped first with



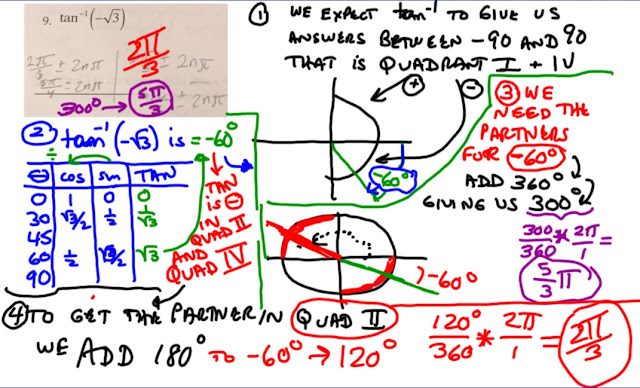 INVERSE TRIG:
INVERSE TRIG: Take the xy-plane and
Take the xy-plane and