
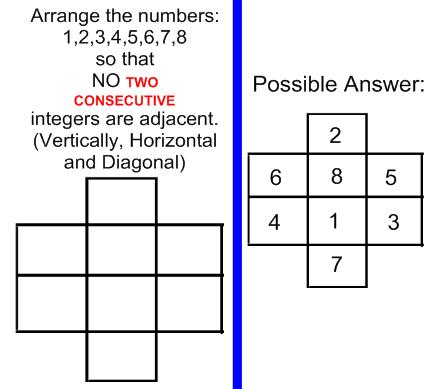
I would like to share some puzzles with the Math Teacher Community.
Please feel free to use any or all of the problems.
I believe my unique method used to award the points will be of interest. When I gave any extra credit points for a puzzle I would offer the same number of points as there was students in the class. (25 students could get 25 points.) Too many points to offer? Well there was a catch. Everyone who got the question correct would share equally in the total number of points available. (Thus, if only 2 got the question correct, then they each got about 25/2 [12 or 13] points. If 5 students were correct, then each student would get only 5 points each. If 13 students were right, then each one got about 2 points. This wrinkle in the distribution of points slowed down the sharing of correct answers within my class!
Puzzle #1
Sometimes called a Word Arithmetic Problem:
You must find the distinct digit that replaces a letter, each time that it appears,
so as to satisfy the arithmetic problem presented.
Given:
SMAX + SMAX + SMAX + SMAX = XAMS
What will "XMAS" equal?
Puzzle #2
The sum of all the positive integer factors of
a certain prime number is 32.
What is this prime number?
Puzzle #3
If a quart and a half of egg nog costs $6.30,
how much would two pints cost?
Puzzle #4
Find the SUM of the following ROMAN NUMERALS:
VII + XIV
Give your answer in Roman Numerals.
Puzzle #5
A REGION bounded by the X-AXIS and the
LINES Y = M X + 4 , and X = 1 and X = 4
has an AREA of 7 square units.
What must be the value for M?
Puzzle #6
Successive DISCOUNTS of 10% and then 20%
are equivalent to what SINGLE DISCOUNT?
*******************************************
ANSWERS:
1) 8172
2) 31
3) $4.20
4) XXI
5) -2/3
6) 28 %
*******************************************
Puzzle #7Please feel free to use any or all of the problems.
I believe my unique method used to award the points will be of interest. When I gave any extra credit points for a puzzle I would offer the same number of points as there was students in the class. (25 students could get 25 points.) Too many points to offer? Well there was a catch. Everyone who got the question correct would share equally in the total number of points available. (Thus, if only 2 got the question correct, then they each got about 25/2 [12 or 13] points. If 5 students were correct, then each student would get only 5 points each. If 13 students were right, then each one got about 2 points. This wrinkle in the distribution of points slowed down the sharing of correct answers within my class!
Puzzle #1
Sometimes called a Word Arithmetic Problem:
You must find the distinct digit that replaces a letter, each time that it appears,
so as to satisfy the arithmetic problem presented.
Given:
SMAX + SMAX + SMAX + SMAX = XAMS
What will "XMAS" equal?
Puzzle #2
The sum of all the positive integer factors of
a certain prime number is 32.
What is this prime number?
Puzzle #3
If a quart and a half of egg nog costs $6.30,
how much would two pints cost?
Puzzle #4
Find the SUM of the following ROMAN NUMERALS:
VII + XIV
Give your answer in Roman Numerals.
Puzzle #5
A REGION bounded by the X-AXIS and the
LINES Y = M X + 4 , and X = 1 and X = 4
has an AREA of 7 square units.
What must be the value for M?
Puzzle #6
Successive DISCOUNTS of 10% and then 20%
are equivalent to what SINGLE DISCOUNT?
*******************************************
ANSWERS:
1) 8172
2) 31
3) $4.20
4) XXI
5) -2/3
6) 28 %
*******************************************
A father has a son.
As of now, their ages total 100.
The father is three times as old as
the son was when the father was
ten years older than the son is now.
How old is the father?
.........................................................
Answer: The father is now 63.
(The best method for solving this
problem is "Guess and Check".
The equations that evolve using
an Algebraic approach are very
messy!)
******************************************
Here is good Christmas Handout:
Separate the SNOWMEN!
(Use only 6 straight lines.)
LINK: Back to Contents








