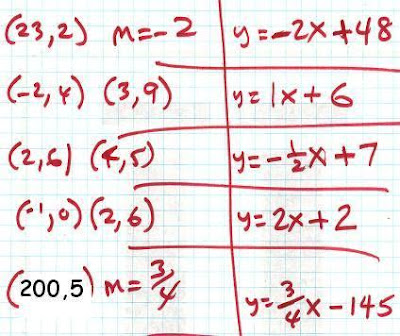LINK: Back to Contents
Instead of memorizing the formulas for Centigrade to Fehrenheit ----
Sunday, December 20, 2009
Monday, December 14, 2009
CALCULUS - graphing f' and f"
LINK: Back to Contents
Comparing f to f' to f"
******************
Example:
If y = Parabola
then y ' = Straight Line
If y = Parabola
then y ' = Straight Line
******************
f = position at time T
f = position at time T
f ' = Velocity
f " = Acceleration
******************
If you are given the Velocity
and asked to find the Distance Traveled
from Time t1 to t2, then INTEGRATE
the Velocity from t1 to t2.
AREA UNDER the VELOCITY!
Tuesday, December 8, 2009
Saturday, December 5, 2009
SLOPE (of a LINE)
FINDING the EQUATION of a LINE
What is this SLOPE THING?
Suppose we want to buy some T-shirts.
same amount. There is a charge
(an initial fee)
for setting up the logo for the order.
and 100 shirts would cost $633.
What is the COST for each shirt?
Dollars per Shirt!
(The SLOPE OF A LINE)
$540 divided by 90 shirts gives
a RATE (Cost per Shirt) of $6.00 per shirt.
Why then do 10 shirts at $6 each cost $93?
Because there is a set-up fee of $33.
The Cost formula that Mr. Smith uses is:
Total Cost = ( $6 ) times # of shirts PLUS $33
We could represent this with the equation:
y = 6 x + 33
(Note: y depends on x for its value!)
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
Take a look at the set of ordered pairs:
{ (3,11) (4,13) (5,15) (6,17)}
We notice that when X changes one unit
(11 to 13). As X changes 2 units (3 to 5),
Y changes 4 units (11 to 15).
NOTE:
We are not saying that the values for y
are twice as big as the values for x.
We are talking about changes in y and x.
We call this the RATE OF CHANGE OF Y
WITH RESPECT TO X. Graphing these points
onto the xy-plane and connecting the points
with a line we have what is called a line
with SLOPE of 2. The EQUATION that these
points SATISFY is y = 2x + 5. Notice the
SLOPE of 2 is situated next to x.
Picking a point on the graph and moving
3 units to the RIGHT (RUN)
and then moving
6 units UP (RISE) we will land
us back onto the line.
The RISE is 6 and the RUN is 3.
the FRACTION (RATIO)
RISE/RUN EQUALS 2.
One definition for the slope of a LINE
m = RISE/RUN.
How about the graph of the equation
y = (3/4)x - 1
Some of the ordered pairs that satisfy
this equation are {(4,2) (8,5) (12,8) ...}
When x changes 4 units, y changes 3 units.
The RATIO of 3 to 4 represents the
change in y with respect to the change in x.
THE CHANGE IN Y over the CHANGE in x is 3/4.
The slope of the graph of this equation is 3/4.
The SLOPE of the graph of the solutions to:
(i) a LINEAR FUNCTION f(x) = mx + b
(ii) an equation in the form Ax + By = C
(iii) or in the form y = mx + b
..........SLOPE is the rate that y changes
with respect to a change in x
..........In other words,
m = (y2-y1) / (x2-x1)
or m = change of y divided by the change in x
-----the values for x change by (x2-x1)
and the corresponding y's change by (y2-y1)

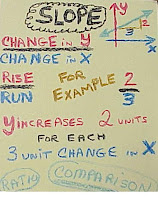
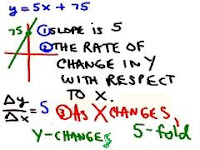
LINK: Back to Contents
Thursday, December 3, 2009
Saturday, November 28, 2009
Logarithms / Exponential Functions
LINK: Back to Contents
Exponential Functions and Logarithmics Functions
are INVERSES of eachother.
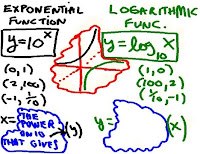 y = log base 10 of x
y = log base 10 of x
Exponential Functions and Logarithmics Functions
are INVERSES of eachother.
 y = log base 10 of x
y = log base 10 of xTuesday, November 24, 2009
Puzzles - using for extra credit

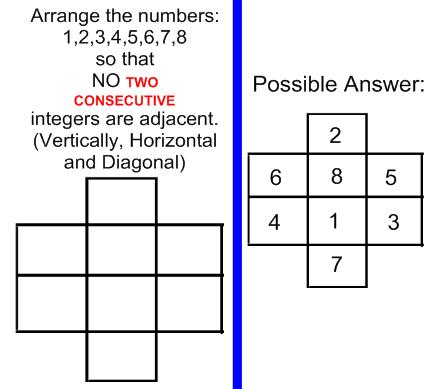
I would like to share some puzzles with the Math Teacher Community.
Please feel free to use any or all of the problems.
I believe my unique method used to award the points will be of interest. When I gave any extra credit points for a puzzle I would offer the same number of points as there was students in the class. (25 students could get 25 points.) Too many points to offer? Well there was a catch. Everyone who got the question correct would share equally in the total number of points available. (Thus, if only 2 got the question correct, then they each got about 25/2 [12 or 13] points. If 5 students were correct, then each student would get only 5 points each. If 13 students were right, then each one got about 2 points. This wrinkle in the distribution of points slowed down the sharing of correct answers within my class!
Puzzle #1
Sometimes called a Word Arithmetic Problem:
You must find the distinct digit that replaces a letter, each time that it appears,
so as to satisfy the arithmetic problem presented.
Given:
SMAX + SMAX + SMAX + SMAX = XAMS
What will "XMAS" equal?
Puzzle #2
The sum of all the positive integer factors of
a certain prime number is 32.
What is this prime number?
Puzzle #3
If a quart and a half of egg nog costs $6.30,
how much would two pints cost?
Puzzle #4
Find the SUM of the following ROMAN NUMERALS:
VII + XIV
Give your answer in Roman Numerals.
Puzzle #5
A REGION bounded by the X-AXIS and the
LINES Y = M X + 4 , and X = 1 and X = 4
has an AREA of 7 square units.
What must be the value for M?
Puzzle #6
Successive DISCOUNTS of 10% and then 20%
are equivalent to what SINGLE DISCOUNT?
*******************************************
ANSWERS:
1) 8172
2) 31
3) $4.20
4) XXI
5) -2/3
6) 28 %
*******************************************
Puzzle #7Please feel free to use any or all of the problems.
I believe my unique method used to award the points will be of interest. When I gave any extra credit points for a puzzle I would offer the same number of points as there was students in the class. (25 students could get 25 points.) Too many points to offer? Well there was a catch. Everyone who got the question correct would share equally in the total number of points available. (Thus, if only 2 got the question correct, then they each got about 25/2 [12 or 13] points. If 5 students were correct, then each student would get only 5 points each. If 13 students were right, then each one got about 2 points. This wrinkle in the distribution of points slowed down the sharing of correct answers within my class!
Puzzle #1
Sometimes called a Word Arithmetic Problem:
You must find the distinct digit that replaces a letter, each time that it appears,
so as to satisfy the arithmetic problem presented.
Given:
SMAX + SMAX + SMAX + SMAX = XAMS
What will "XMAS" equal?
Puzzle #2
The sum of all the positive integer factors of
a certain prime number is 32.
What is this prime number?
Puzzle #3
If a quart and a half of egg nog costs $6.30,
how much would two pints cost?
Puzzle #4
Find the SUM of the following ROMAN NUMERALS:
VII + XIV
Give your answer in Roman Numerals.
Puzzle #5
A REGION bounded by the X-AXIS and the
LINES Y = M X + 4 , and X = 1 and X = 4
has an AREA of 7 square units.
What must be the value for M?
Puzzle #6
Successive DISCOUNTS of 10% and then 20%
are equivalent to what SINGLE DISCOUNT?
*******************************************
ANSWERS:
1) 8172
2) 31
3) $4.20
4) XXI
5) -2/3
6) 28 %
*******************************************
A father has a son.
As of now, their ages total 100.
The father is three times as old as
the son was when the father was
ten years older than the son is now.
How old is the father?
.........................................................
Answer: The father is now 63.
(The best method for solving this
problem is "Guess and Check".
The equations that evolve using
an Algebraic approach are very
messy!)
******************************************
Here is good Christmas Handout:
Separate the SNOWMEN!
(Use only 6 straight lines.)
LINK: Back to Contents
Saturday, November 21, 2009
Math in Nature - Fibonacci
Fibonacci Sequence:
0,1,1,2,3,5,8,13,21,34,...
(add two adjacent terms to get the following term!)
There is a great website to see
1) Is 13 really that unlucky?
2) Why do we consider 21 as ADULTHOOD?
3) Why do we use 3 by 5 cards for notes?
4) Is a 5 by 8 inch photo visually appealing to you?
5) The Mountain Laurel Blossom (found in the Smokies)
has the shape of a Pentagon! (5 sided)
Maybe SIGNS are not considered Nature,
but we find them in our world.
First let's review the names of polygons:
NOW A FEW SIGN EXAMPLES:


Below is the bottom of a stalk of CELERY.
(Check out the SYMMETRY!)
Fibonacci Numbers and Nature :
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html

LINK: Back to the contents of the entire blog...
Wednesday, November 18, 2009
MATRICES
LINK: Back to Contents
Arranging numbers in a Rectangular Form
is an integral part of a spreadsheet.
Mathematics has been using this style
before computers existed. The MATRIX
is a RECTANGULAR ARRAY OF NUMBERS.
The DIMENSION of a Matrix has two
numbers the first reflects the
number of rows and the second number
represents the number of columns.
Here is a matrix with
three rows and two columns:
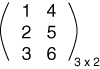
Here is a link to a great Matrix Site:
INVERSE MATRICES
(only exist for a SQUARE MATRIX)
are used to solve Simultaneous Equations
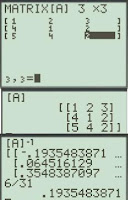
A=[1 2 3; 4 1 2; 5 4 2]
A =
1 2 3
4 1 2
5 4 2
inv(A)=
-6/31 8/31 1/31
2/31 -13/31 10/31
11/31 6/31 -7/31
Arranging numbers in a Rectangular Form
is an integral part of a spreadsheet.
Mathematics has been using this style
before computers existed. The MATRIX
is a RECTANGULAR ARRAY OF NUMBERS.
The DIMENSION of a Matrix has two
numbers the first reflects the
number of rows and the second number
represents the number of columns.
Here is a matrix with
three rows and two columns:
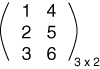
Here is a link to a great Matrix Site:
INVERSE MATRICES
(only exist for a SQUARE MATRIX)
are used to solve Simultaneous Equations
A=[1 2 3; 4 1 2; 5 4 2]
A =
1 2 3
4 1 2
5 4 2
inv(A)=
-6/31 8/31 1/31
2/31 -13/31 10/31
11/31 6/31 -7/31

Subscribe to:
Comments (Atom)